(本小题满 分12分)
分12分)
已知向量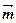 =(1,1),向量
=(1,1),向量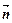 与向量
与向量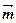 夹角为
夹角为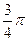 ,且
,且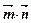 =-1.
=-1.
(1)求向量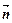 ;
;
(2)若向量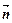 与向量
与向量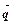 =(1,0)的夹角为
=(1,0)的夹角为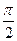 ,向量
,向量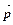 =(cosA,2cos2
=(cosA,2cos2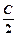 ),其中A、B、C为△ABC的内角,且B=60°,求|
),其中A、B、C为△ABC的内角,且B=60°,求|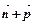 |的取值范围;
|的取值范围;
推荐套卷
(本小题满 分12分)
分12分)
已知向量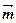 =(1,1),向量
=(1,1),向量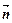 与向量
与向量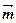 夹角为
夹角为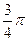 ,且
,且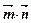 =-1.
=-1.
(1)求向量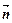 ;
;
(2)若向量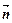 与向量
与向量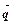 =(1,0)的夹角为
=(1,0)的夹角为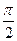 ,向量
,向量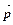 =(cosA,2cos2
=(cosA,2cos2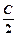 ),其中A、B、C为△ABC的内角,且B=60°,求|
),其中A、B、C为△ABC的内角,且B=60°,求|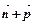 |的取值范围;
|的取值范围;