【必做题】第22题和第23题为必做题, 每小题10分,共20分.要写出必要的文字说明或演算步骤.
有甲、乙两个箱子,甲箱 中有
中有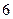 张卡片,其中
张卡片,其中 张写有数字
张写有数字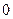 ,
, 张写有数字
张写有数字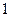 ,
, 张写有数字
张写有数字 ;乙箱中也有
;乙箱中也有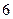 张卡片,其中
张卡片,其中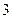 张写有数
张写有数 字
字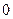 ,
, 张写有数字
张写有数字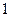 ,
,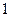 张写有数字
张写有数字 .
.
(1)如果从甲、乙箱中各取一张卡片,设取出的 张卡片上数字之积为
张卡片上数字之积为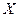 ,求
,求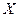 的
的
分布列及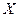 的
的 数学期望;
数学期望;
(2)如果从甲箱中取一张卡片,从乙箱中取两张卡片,那么取出的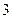 张卡片都写有
张卡片都写有
数字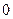 的概率是多少?
的概率是多少?
推荐套卷
【必做题】第22题和第23题为必做题, 每小题10分,共20分.要写出必要的文字说明或演算步骤.
有甲、乙两个箱子,甲箱 中有
中有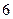 张卡片,其中
张卡片,其中 张写有数字
张写有数字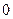 ,
, 张写有数字
张写有数字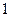 ,
, 张写有数字
张写有数字 ;乙箱中也有
;乙箱中也有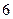 张卡片,其中
张卡片,其中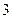 张写有数
张写有数 字
字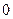 ,
, 张写有数字
张写有数字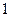 ,
,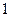 张写有数字
张写有数字 .
.
(1)如果从甲、乙箱中各取一张卡片,设取出的 张卡片上数字之积为
张卡片上数字之积为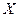 ,求
,求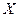 的
的
分布列及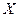 的
的 数学期望;
数学期望;
(2)如果从甲箱中取一张卡片,从乙箱中取两张卡片,那么取出的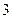 张卡片都写有
张卡片都写有
数字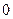 的概率是多少?
的概率是多少?