已知向量 a
a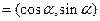 ,b
,b 且a,b满足|ka+b |=
且a,b满足|ka+b |= |a-kb|
|a-kb|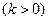 ,
,
(1)求a与b的数量积用k表示的解析式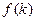 ;
;
(2) a能否和b垂直?a能否和b平行?若不能,请说明理由;若能,请求出相应的k值;
(3)求向量a与向量b的夹角的最大值。
推荐套卷
已知向量 a
a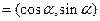 ,b
,b 且a,b满足|ka+b |=
且a,b满足|ka+b |= |a-kb|
|a-kb|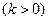 ,
,
(1)求a与b的数量积用k表示的解析式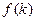 ;
;
(2) a能否和b垂直?a能否和b平行?若不能,请说明理由;若能,请求出相应的k值;
(3)求向量a与向量b的夹角的最大值。