设椭圆 :
: ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合, 与椭圆交于
与椭圆交于 ,当
,当 与
与 轴垂直时,
轴垂直时,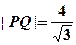 ,
, 为椭圆的右焦点,
为椭圆的右焦点, 为椭圆
为椭圆 上任意一点,若
上任意一点,若 面积的最大值为
面积的最大值为 。
。
(1)求椭圆 的方程;
的方程;
(2)直线 绕着
绕着 旋转,与圆
旋转,与圆 :
: 交于
交于 两点,若
两点,若 ,求
,求 的面积
的面积 的取值范围。
的取值范围。
推荐套卷
设椭圆 :
: ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合, 与椭圆交于
与椭圆交于 ,当
,当 与
与 轴垂直时,
轴垂直时,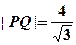 ,
, 为椭圆的右焦点,
为椭圆的右焦点, 为椭圆
为椭圆 上任意一点,若
上任意一点,若 面积的最大值为
面积的最大值为 。
。
(1)求椭圆 的方程;
的方程;
(2)直线 绕着
绕着 旋转,与圆
旋转,与圆 :
: 交于
交于 两点,若
两点,若 ,求
,求 的面积
的面积 的取值范围。
的取值范围。