（本小题满分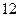
分）
桌面上有两颗均匀的骰子（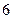
个面上分别标有数字
）.将桌面上骰子全部抛掷在桌面上，然后拿掉那些朝上点数为奇数的骰子，如果桌面上没有了骰子，停止抛掷，如果桌面上还有骰子，继续抛掷桌面上的剩余骰子. 记抛掷两次之内（含两次）去掉的骰子的颗数为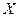
.
（Ⅰ）求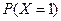
；
（Ⅱ）求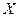的分布列及期望 
.
相关试题
集合
求函数
的解析式；
,且
设
上的最大值、最小值分别为
，记
，求
的最小值.
（其中
为常数且
）的图象经过点
.
的解析式；
在
上恒成立，求实数
的取值范围.
，
,函数
的定义域为
；
。
.
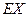推荐套卷
（本小题满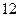分分）
桌面上有两颗均匀的骰子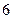（个面上分别标有数字）.将桌面上骰子全部抛掷在桌面上，然后拿掉那些朝上点数为奇数的骰子，如果桌面上没有了骰子，停止抛掷，如果桌面上还有骰子，继续抛掷桌面上的剩余骰子. 记抛掷两次之内（含两次）去掉的骰子的颗数为.
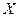（Ⅰ）求；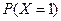
（Ⅱ）求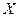的分布列及期望 .
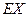粤公网安备 44130202000953号