（（本小题满分12分）
已知点A（1，1）是椭圆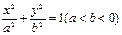
上一点，F1、F2是椭圆的两焦点，且满足|AF1|+|AF2|=4。
（I）求椭圆的标准方程；
（II）过点A（1，1）与椭圆相切的直线方程；
（III）设点C、D是椭圆上两点，直线AC、AD的倾斜角互补，试判断直线CD的斜率是否为定值？若是定值，求出定值；若不是定值，说明理由。
和
，并且过点
，求椭圆的方程。
上的点的横坐标变为原来的2倍，纵坐标变为原来的一半，求所得曲线的方程。
是两个定点，以
为一条底边作梯形
，使
的长为定值，
与
的长之和也是定值，则
点的轨迹是什么曲线？
为圆心、半径为
的一个圆内有一个定点
且
，如果圆
过定点
和定直线
，动圆
过推荐套卷
（（本小题满分12分）
已知点A（1，1）是椭圆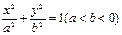上一点，F1、F2是椭圆的两焦点，且满足|AF1|+|AF2|=4。
（I）求椭圆的标准方程；
（II）过点A（1，1）与椭圆相切的直线方程；
（III）设点C、D是椭圆上两点，直线AC、AD的倾斜角互补，试判断直线CD的斜率是否为定值？若是定值，求出定值；若不是定值，说明理由。
粤公网安备 44130202000953号