((本小题满分12分)
椭圆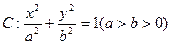 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=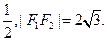
(I)求椭圆C的方程。
(II)以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由。
推荐套卷
((本小题满分12分)
椭圆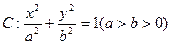 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=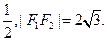
(I)求椭圆C的方程。
(II)以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由。