(本小题满分12分)
已知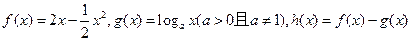 在定义域上为减函数,且其导函数
在定义域上为减函数,且其导函数 存在零点。
存在零点。
(I)求实数a的值;
(II)函数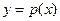 的图象与函数
的图象与函数 的图象关于直线y=x对称,且
的图象关于直线y=x对称,且 为函数
为函数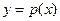 的导函数,
的导函数,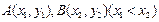 是函数
是函数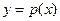 图像上两点,若
图像上两点,若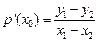 ,判断
,判断 的大小,并证明你的结论。[
的大小,并证明你的结论。[
推荐套卷
(本小题满分12分)
已知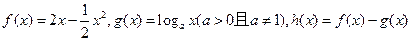 在定义域上为减函数,且其导函数
在定义域上为减函数,且其导函数 存在零点。
存在零点。
(I)求实数a的值;
(II)函数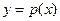 的图象与函数
的图象与函数 的图象关于直线y=x对称,且
的图象关于直线y=x对称,且 为函数
为函数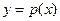 的导函数,
的导函数,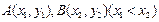 是函数
是函数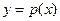 图像上两点,若
图像上两点,若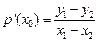 ,判断
,判断 的大小,并证明你的结论。[
的大小,并证明你的结论。[