已知点F(0, 1)，直线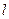
: 
，圆C: 
.
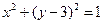（Ⅰ） 若动点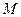
到点F的距离比它到直线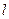的距离小1，求动点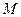的轨迹E的方程；
（Ⅱ） 过轨迹E上一点P作圆C的切线，切点为A、B，当四边形PACB的面积S最小时，求点P的坐标及S的最小值。
相关试题
（2）若
，且
，求
的取值范围
, 求
及
的值.
，
，且
满足关系
（其中
）
与
的数量积表示为关于
的函数
；
的最大值.
的最小正周期为
的值；
的图像上各点的横坐标缩短到原来的
，纵坐标不变，得到函数
的图像，求函数
上的最小值推荐套卷
已知点F(0, 1)，直线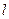: ，圆C: .
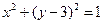（Ⅰ） 若动点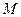到点F的距离比它到直线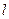的距离小1，求动点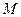的轨迹E的方程；
（Ⅱ） 过轨迹E上一点P作圆C的切线，切点为A、B，当四边形PACB的面积S最小时，求点P的坐标及S的最小值。
粤公网安备 44130202000953号