（本小题满分12分）
如图，在斜边为AB的Rt△ABC，过A作PA⊥平面ABC，AE⊥PB于E，AF⊥PC于F．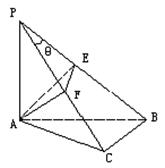
(1)求证：BC⊥平面PAC．
(2)求证：PB⊥平面AEF．
(3)若AP=AB=2，试用tgθ(∠BPC=θ)表示△AEF的面积、当tgθ取何值时，△AEF的面积最大？最大面积是多少？
推荐套卷
（本小题满分12分）
如图，在斜边为AB的Rt△ABC，过A作PA⊥平面ABC，AE⊥PB于E，AF⊥PC于F．
(1)求证：BC⊥平面PAC．
(2)求证：PB⊥平面AEF．
(3)若AP=AB=2，试用tgθ(∠BPC=θ)表示△AEF的面积、当tgθ取何值时，△AEF的面积最大？最大面积是多少？
粤公网安备 44130202000953号