如图所示的测量旗杆的方法，已知AB是标杆，BC表示AB在太阳光下的影
子，叙述错误的是（ ）
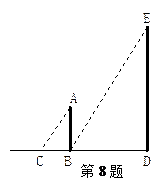
A．可以利用在同一时刻，不同物
体与其影长的比相等来计算旗杆的高
B．只需测
量出标杆和旗杆的影长就可计算出旗杆的高
C
．可以利用△ABC∽△EDB
，来计算旗杆的高
D．需要测量出AB、BC和DB的长，才能计算出旗杆的高
相关试题
的根是（）
的一次项是（）
是方程
的根，则
的值（ ）
根的情况（ ）相关知识点
推荐套卷
如图所示的测量旗杆的方法，已知AB是标杆，BC表示AB在太阳光下的影子，叙述错误的是（ ）
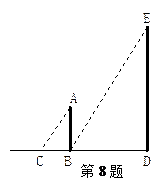
A．可以利用在同一时刻，不同物体与其影长的比相等来计算旗杆的高
B．只需测量出标杆和旗杆的影长就可计算出旗杆的高
C．可以利用△ABC∽△EDB，来计算旗杆的高
D．需要测量出AB、BC和DB的长，才能计算出旗杆的高
粤公网安备 44130202000953号