（本小题满分14分）
如图，在五棱锥P—ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，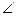 
ABC=45°，AB=2
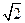，BC=2AE=4，三角形PAB是等腰三角形．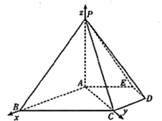
（I）求证：平面PCD⊥平面PAC；
（II）求四棱锥P—ACDE的体积．
的定义域为
，且
时，
时，
．
，解答下述问题：
的取值范围；
，求实数
，集合
．
时，求
；
，求实数
的取值范围；
，求实数
；
，集合
，集合
；
，求实数
的取值范围；推荐套卷
（本小题满分14分）
如图，在五棱锥P—ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC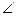， ABC=45°，AB=2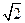，BC=2AE=4，三角形PAB是等腰三角形．
（I）求证：平面PCD⊥平面PAC；
（II）求四棱锥P—ACDE的体积．
粤公网安备 44130202000953号