（本大题９分）
求满足下列条件的直线方程：
(1)经过点P(2，-1)且与直线2x+3y+12=0平行；
(2)经过点Q(-1，3)且与直线x+2y-1=0垂直；
(3)经过点M(1，2)且与点A(2,3)、B(4,-5)距离相等；
(4)经过点N(-1,
3)且在
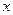轴的截距与它在y轴上的截距的和为零.
相关试题
的前
项和
满足
．
；
为等比数列，并求出
＝9S2，
的图像一部分如图所示，
图像。
，求
的值。
，
是函数的一个周期。推荐套卷
（本大题９分）
求满足下列条件的直线方程：
(1)经过点P(2，-1)且与直线2x+3y+12=0平行；
(2)经过点Q(-1，3)且与直线x+2y-1=0垂直；
(3)经过点M(1，2)且与点A(2,3)、B(4,-5)距离相等；
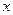(4)经过点N(-1,3)且在轴的截距与它在y轴上的截距的和为零.
粤公网安备 44130202000953号