（本小题满分14分）
一个暗箱里放着6个黑球、4个白球．
（1）依次取出3个球，不放回，若第1次取出的是白球，求第3次取到黑球的概率；
（2）有放回地依次取出3个球，若第1次取出的是白球，求第3次取到黑球的概率；
（3）有放回地依次取出3个球，求取到白球个数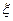
的分布列和期望．
相关试题
，且
。
的值；
与
平行时，求实数
的值。
，求证：
；
垂直，求
的值；
的最大值。
，求函数
的最小正周期及图像的对称轴方程；
，
，求：实数
的值。
，它们的夹角为
，点C是以O为圆心的劣弧
的中点。
的值；（2）
的值。
的图象以
轴
为对称轴，已知
，而且若点
在
的图象上，则点
在函数
的图象上
的解析式
，问是否存在实数
，使
在
内是减函数，在
内是增函数。推荐套卷
（本小题满分14分）
一个暗箱里放着6个黑球、4个白球．
（1）依次取出3个球，不放回，若第1次取出的是白球，求第3次取到黑球的概率；
（2）有放回地依次取出3个球，若第1次取出的是白球，求第3次取到黑球的概率；
（3）有放回地依次取出3个球，求取到白球个数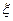的分布列和期望．
粤公网安备 44130202000953号