（本小题满分12分）
某超市为了响应环保要求，鼓励顾客自带购物袋到超市购物，采取了如下措施：对不使用超市塑料购物袋的顾客，超市给予0．96折优惠；对需要超市塑料购物袋的顾客，既要付购买费，也不享受折扣优惠．假
设该超市在某个时段内购物的人数为36人，其中有12位顾客自己带了购物袋，现从这36人中随机抽取2人．
（Ⅰ）求这2人都享受折扣优惠或都不享受折扣优惠的概率；
（Ⅱ）设这2人中享受折扣优惠的人数为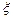
，求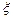的分布列和数学期望．
相关试题
的两个焦点，M是双曲线上一点，且
，求三角形△F1MF2的面积．
中，侧面
与侧面
均为等边三角形，
，
为
中点．
平面
；
的余弦值．（本题12分）
的展开式中，求：（1）第5项的二项式系数;（2）第5项的系数;（3）倒数第3项;（4）含
的项。 （本题12分）
是等腰直角三角形，
是 
面
；
和
推荐套卷
（本小题满分12分）
某超市为了响应环保要求，鼓励顾客自带购物袋到超市购物，采取了如下措施：对不使用超市塑料购物袋的顾客，超市给予0．96折优惠；对需要超市塑料购物袋的顾客，既要付购买费，也不享受折扣优惠．假设该超市在某个时段内购物的人数为36人，其中有12位顾客自己带了购物袋，现从这36人中随机抽取2人．
（Ⅰ）求这2人都享受折扣优惠或都不享受折扣优惠的概率；
（Ⅱ）设这2人中享受折扣优惠的人数为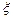，求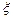的分布列和数学期望．
粤公网安备 44130202000953号