、从某高校新生中随机抽取100名学生，测得身高情况(单位:
)并根据身高评定
其发育标准如右表所示：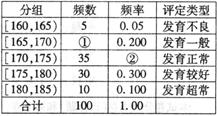
(1)请在频率分布表中的①、②位置上填上相应的数据，估计该批新生中发育正常或较好的概率；
(2)按身高分层抽样，现已抽取20人准备参加世博会志愿者活动，其中有3名学生担任迎宾工作，记“这3名学生中身高低于170的人数
”为
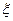，求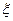的分布列及期望.
，
，
，求
边所在直线的方程，以及该边上中线所在直线的方程．
，
，
，试求点
的坐标，使四边形
为等腰梯形．
，一条边所在的直线的方程是
，求正方形其他三边所在直线的方程．
，
，试讨论：
的条件是什么？（２）
的条件是什么？
，
，求线段
的垂直平分线的方程．推荐套卷
、从某高校新生中随机抽取100名学生，测得身高情况(单位:)并根据身高评定其发育标准如右表所示：
(1)请在频率分布表中的①、②位置上填上相应的数据，估计该批新生中发育正常或较好的概率；
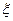(2)按身高分层抽样，现已抽取20人准备参加世博会志愿者活动，其中有3名学生担任迎宾工作，记“这3名学生中身高低于170的人数”为，求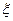的分布列及期望.
粤公网安备 44130202000953号