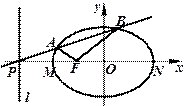(本小题满分12分)
如图,设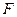 是椭圆
是椭圆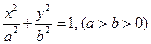 的左焦点,直线
的左焦点,直线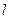 为对应的准线,直线
为对应的准线,直线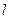 与
与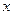 轴交于
轴交于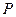 点,
点,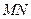 为椭圆的长轴,已知
为椭圆的长轴,已知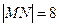 ,且
,且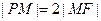 .
.
(1)求椭圆的标准方程;
(2)求证:对于任意的割线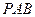 ,恒有
,恒有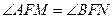 ;
;
(3)求三角形△ABF面积的最大值.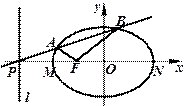
推荐套卷
(本小题满分12分)
如图,设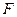 是椭圆
是椭圆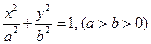 的左焦点,直线
的左焦点,直线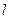 为对应的准线,直线
为对应的准线,直线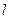 与
与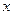 轴交于
轴交于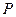 点,
点,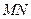 为椭圆的长轴,已知
为椭圆的长轴,已知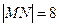 ,且
,且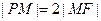 .
.
(1)求椭圆的标准方程;
(2)求证:对于任意的割线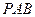 ,恒有
,恒有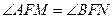 ;
;
(3)求三角形△ABF面积的最大值.