(本小题满分13分)
某军事院校招生要经过考试和体检两个过程,在考试通过后才有体检的机会,两项都合格则被录取.若甲、乙、丙三名考生能通过考试的概率分别为0.4,0.5,0.8,体检合格的概率分别为0.5,0.4,0.25,每名考生是否被录取相互之间没有影响.
(1)求恰有一人通过考试的概率;
(2)设被录取的人数为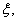 求
求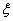 的分布列和数学期望.
的分布列和数学期望.
推荐套卷
(本小题满分13分)
某军事院校招生要经过考试和体检两个过程,在考试通过后才有体检的机会,两项都合格则被录取.若甲、乙、丙三名考生能通过考试的概率分别为0.4,0.5,0.8,体检合格的概率分别为0.5,0.4,0.25,每名考生是否被录取相互之间没有影响.
(1)求恰有一人通过考试的概率;
(2)设被录取的人数为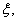 求
求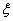 的分布列和数学期望.
的分布列和数学期望.