(本小题共12分)（注意:在试题卷上作答无效）
如图，四棱锥S -ABCD
的底面是边长为3的正方形，SD丄底面ABCD,SB=
,点E、G分别在AB、SC上,且
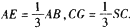
(1) 证明:BC//平面SDE;
(2) 求面SAD与面SBC所成二面角的大小.
，求直平行六面体的侧面积．
求证：
．
上一点，左、右焦点分别为F1，F2。
，求
之值。推荐套卷
(本小题共12分)（注意:在试题卷上作答无效）如图，四棱锥S -ABCD的底面是边长为3的正方形，SD丄底面ABCD,SB=,点E、G分别在AB、SC上,且
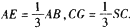
(1) 证明:BC//平面SDE;
(2) 求面SAD与面SBC所成二面角的大小.
粤公网安备 44130202000953号