((本小题满分12分)
已知数列 是公差为
是公差为 的等差数列,
的等差数列, 为其前
为其前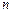 项和。
项和。
(1)若 ,
, ,
, 依次成等比数列,求其公比
依次成等比数列,求其公比 ;
;
(2)若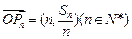 ,求证:对任意的
,求证:对任意的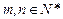 ,向量
,向量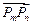 与向量
与向量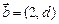 共线;
共线;
(3)若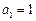 ,
, ,
, ,问是否存在一个半径最小的圆,使得对任意的
,问是否存在一个半径最小的圆,使得对任意的 ,点
,点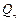 都在这个圆内或圆周上。
都在这个圆内或圆周上。
推荐套卷
((本小题满分12分)
已知数列 是公差为
是公差为 的等差数列,
的等差数列, 为其前
为其前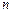 项和。
项和。
(1)若 ,
, ,
, 依次成等比数列,求其公比
依次成等比数列,求其公比 ;
;
(2)若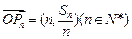 ,求证:对任意的
,求证:对任意的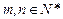 ,向量
,向量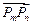 与向量
与向量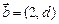 共线;
共线;
(3)若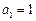 ,
, ,
, ,问是否存在一个半径最小的圆,使得对任意的
,问是否存在一个半径最小的圆,使得对任意的 ,点
,点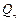 都在这个圆内或圆周上。
都在这个圆内或圆周上。