已知数列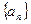
首项
，公比为
的等比数列，又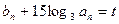
，常数
，数列
满足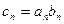
，
（1）、求证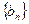
为等差数列；
（2）、若是递减数列，求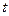
的最小值；（参考数据：
）
（3）、是否存在正整数
，使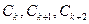
重新排列后成等比数列，若存在，求
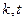的值，若不存在，说明理由。
,其中
,
，求实数
的取值范围
，若函数
，其中
，当
时，其值域为
，求实数
的值。
，如果函数
在
上的最大值为
，求
的值。
，
，试比较
与
的大小关系。推荐套卷
已知数列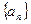首项，公比为的等比数列，又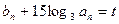，常数，数列满足，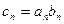
（1）、求证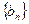为等差数列；
（2）、若是递减数列，求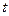的最小值；（参考数据：）
（3）、是否存在正整数，使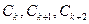重新排列后成等比数列，若存在，求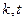的值，若不存在，说明理由。
粤公网安备 44130202000953号