(本小题满分14分)已知定义在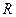 上的函数
上的函数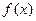 ,满足条件:①
,满足条件:①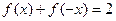 ,②对非零实数
,②对非零实数 ,都有
,都有 .
.
(1)求函数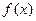 的解析式;
的解析式;
(2)设函数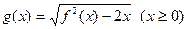 ,直线
,直线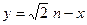 分别与函数
分别与函数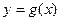 ,
, 交于
交于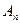 、
、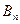 两点,(其中
两点,(其中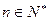 );设
);设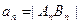 ,
, 为数列
为数列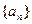 的前
的前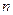 项和,求证:当
项和,求证:当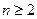 时,
时,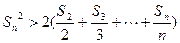 .
.
推荐套卷
(本小题满分14分)已知定义在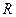 上的函数
上的函数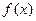 ,满足条件:①
,满足条件:①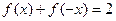 ,②对非零实数
,②对非零实数 ,都有
,都有 .
.
(1)求函数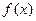 的解析式;
的解析式;
(2)设函数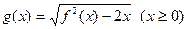 ,直线
,直线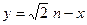 分别与函数
分别与函数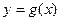 ,
, 交于
交于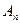 、
、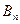 两点,(其中
两点,(其中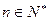 );设
);设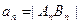 ,
, 为数列
为数列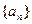 的前
的前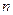 项和,求证:当
项和,求证:当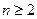 时,
时,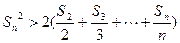 .
.