(本小题满分14分)
已知椭圆C的长轴长与短轴长之比为 ,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
(1)求椭圆C的标准方程;
(2)已知A(-3,0),B(3,0)P是椭圆C上异于A、B的任意一点,直线AP、BP分别交于y轴于M、N两点,求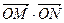 的值;
的值;
(3)在(2)的条件下,若G(s,o)、H(k,o)且 ,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
推荐套卷
(本小题满分14分)
已知椭圆C的长轴长与短轴长之比为 ,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
(1)求椭圆C的标准方程;
(2)已知A(-3,0),B(3,0)P是椭圆C上异于A、B的任意一点,直线AP、BP分别交于y轴于M、N两点,求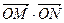 的值;
的值;
(3)在(2)的条件下,若G(s,o)、H(k,o)且 ,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.