（（本小题满分12分）
已知几何体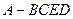
的三视图如图所示，其中侧视图和俯视图都是腰长为4的等腰直角三角形，正视图为直角梯形.求：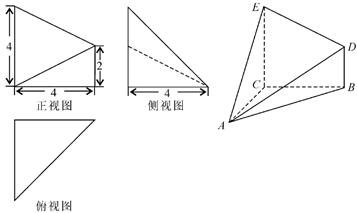
（1）异面直线
与
所成角的余弦值；
（2）二面角
的正弦值；
（3）此几何体的体积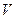
的大小.
相关试题
的方程为
，求直线
的方程，使得：（１）
；（２）
是
的边
上的点，且
．
与
互相平行，且
，
之间的距离为
，求直线
，点
，求证：
，且平行于直线
的直线方程是
；
．相关知识点
推荐套卷
（（本小题满分12分）
已知几何体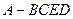的三视图如图所示，其中侧视图和俯视图都是腰长为4的等腰直角三角形，正视图为直角梯形.求：
（1）异面直线与所成角的余弦值；
（2）二面角的正弦值；
（3）此几何体的体积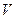的大小.
粤公网安备 44130202000953号