在平面直角坐标系xOy中,反比例函数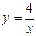
的图象与抛物线
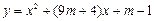交于点A(3, n). 
（1）求n的值及抛物线的解析式；
（2） 过点A作直线BC，交x轴于点B，交反比例函数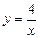
（
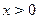）的图象于点C，且AC=2AB，求B、C两点的坐标；
（3）在（2）的条件下，若点P是抛物线对称轴上的一点，且点P到x轴和直线BC的距离相等，求点P的坐标.
；（3）
；（4）0.16．
； ⑶ 1.69
；（2）
．
相关知识点
推荐套卷
在平面直角坐标系xOy中,反比例函数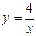的图象与抛物线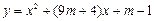交于点A(3, n).
（1）求n的值及抛物线的解析式；
（2） 过点A作直线BC，交x轴于点B，交反比例函数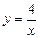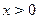（）的图象于点C，且AC=2AB，求B、C两点的坐标；
（3）在（2）的条件下，若点P是抛物线对称轴上的一点，且点P到x轴和直线BC的距离相等，求点P的坐标.
粤公网安备 44130202000953号