（本小题满分14分）
设函数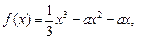
.
(1) 试问函数f(x)能否在x=-1时取得极值？说明理由；
(2) 若a=-1，当x∈［-3,4］时，函数f(x)与g(x)的图像有两个公共点，求c的取值范围.
相关试题
,
的最大值是1，其图像经过点
.
的解析式；
，求它的外接球的体积。
和400π
，其中
时，判断函数
在定义域上的单调性；
，不等式
都成立。相关知识点
推荐套卷
（本小题满分14分）
设函数.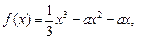
(1) 试问函数f(x)能否在x=-1时取得极值？说明理由；
(2) 若a=-1，当x∈［-3,4］时，函数f(x)与g(x)的图像有两个公共点，求c的取值范围.
粤公网安备 44130202000953号