某射手每次射击击中目标的概率是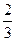 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标。另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击, 击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而
击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而 另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记
另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记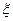 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求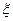 的分布列。
的分布列。
推荐套卷
某射手每次射击击中目标的概率是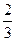 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标。另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击, 击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而
击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而 另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记
另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记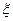 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求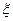 的分布列。
的分布列。