(本小题满分13分)退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]绘制频率分布直方图,如图所示.若规定年龄分布在[20,40)岁的人为“青年人”,[40,60)为“中年人”, [60,80]为“老年人”.
(Ⅰ)若每一组数据的平均值用该区间中点值来代替,试估算所调查的600人的平均年龄;
(Ⅱ)将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率.从该城市20-80年龄段市民中随机抽取3人,记抽到“老年人”的人数为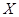 ,求随机变量
,求随机变量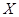 的分布列和数学期望.
的分布列和数学期望.