椭圆E的中心在原点O，焦点在x轴上，离心率e=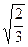
，过点C(-1，0)的直线
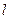交椭圆于A，B两点，且满足
，
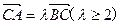为常数。
（1）当直线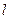的斜率k=1且
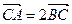时，求三角形OAB的面积.
（2）当三角形OAB的面积取得最大值时，求椭圆E的方程.
相关试题
，
分别为等差、等比数列，且
．
，求数列
的前n项和．
的前
项和
，且
．
，求证：
是等比数列，并求其前
．
是以向量
为边的平行四边形，又
，试用
表示
。
，且
为第三象限角．
的值；
的值
中，
；
，求
边上的高．推荐套卷
椭圆E的中心在原点O，焦点在x轴上，离心率e=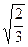，过点C(-1，0)的直线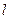交椭圆于A，B两点，且满足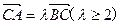，为常数。
（1）当直线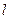的斜率k=1且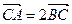时，求三角形OAB的面积.
（2）当三角形OAB的面积取得最大值时，求椭圆E的方程.
粤公网安备 44130202000953号