(本小题14分)
已知直线L被两平行直线 :
: 与
与 :
: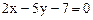 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线 上,已知
上,已知 圆
圆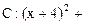
 .
.
(Ⅰ)求两平行直线 与
与 的距离;
的距离;
(Ⅱ)证明直线L与圆C恒有两个交 点;
点; (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
.
推荐套卷
(本小题14分)
已知直线L被两平行直线 :
: 与
与 :
: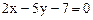 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线 上,已知
上,已知 圆
圆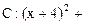
 .
.
(Ⅰ)求两平行直线 与
与 的距离;
的距离;
(Ⅱ)证明直线L与圆C恒有两个交 点;
点; (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
.