设椭圆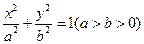
的左,右焦点为
，
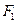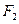，（１，
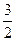）为椭圆上一点，椭圆的
长半轴长等于焦距，曲线Ｃ是以坐标原点为顶点，以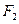为焦点的抛物线，自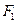引直线交曲线Ｃ于Ｐ，Ｑ两个不同的交点，点Ｐ关于
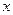轴的对称点记为Ｍ，设
．
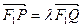（1）求椭圆方程和抛物线方程；
（2）证明：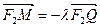
；
（3）若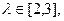
求|ＰＱ|的取值范围
，集合B=
．
；
，且
，求m的取值范围．
．
的值；
时，求
的值．
，AD是BC边上的高，AD＝
，BC＝2.
的值
，其中
.
//
,求
的值；
的大小
，试求 
的值．推荐套卷
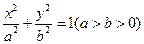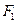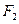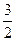设椭圆的左,右焦点为，，（１，）为椭圆上一点，椭圆的
长半轴长等于焦距，曲线Ｃ是以坐标原点为顶点，以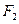为焦点的抛物线，自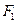引直线交曲线Ｃ于Ｐ，Ｑ两个不同的交点，点Ｐ关于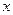轴的对称点记为Ｍ，设．
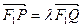（1）求椭圆方程和抛物线方程；
（2）证明：；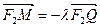
（3）若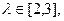求|ＰＱ|的取值范围
粤公网安备 44130202000953号