(本题满分18分,第1小题满分6分,第2小题满分6分,第3小题满分6分)
已知函数 ,如果存在给定的实数对(
,如果存在给定的实数对( ),使得
),使得 恒成立,则称
恒成立,则称 为“S-函数”.
为“S-函数”.
(1)判断函数 是否是“S-函数”;
是否是“S-函数”;
(2)若 是一个“S-函数”,求出所有满足条件的有序实数对
是一个“S-函数”,求出所有满足条件的有序实数对 ;
;
(3)若定义域为 的函数
的函数 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对 和
和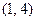 ,当
,当 时,
时, 的值域为
的值域为 ,求当
,求当 时函数
时函数 的值域.
的值域.
推荐套卷
(本题满分18分,第1小题满分6分,第2小题满分6分,第3小题满分6分)
已知函数 ,如果存在给定的实数对(
,如果存在给定的实数对( ),使得
),使得 恒成立,则称
恒成立,则称 为“S-函数”.
为“S-函数”.
(1)判断函数 是否是“S-函数”;
是否是“S-函数”;
(2)若 是一个“S-函数”,求出所有满足条件的有序实数对
是一个“S-函数”,求出所有满足条件的有序实数对 ;
;
(3)若定义域为 的函数
的函数 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对 和
和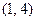 ,当
,当 时,
时, 的值域为
的值域为 ,求当
,求当 时函数
时函数 的值域.
的值域.