经过调查发现,某种新产品在投放市场的100天中,前40天,其价格直线上升,(价格是关于时间的一次函数),而后60天,其价格则呈直线下降趋势,现抽取其中4天的价格如下表所示:
| 时间 |
第4天 |
第32天 |
第60天 |
第90天 |
| 价格(千元) |
23 |
30 |
22 |
7 |
(Ⅰ)写出价格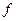 (
(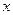 )关于时间
)关于时间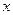 的函数表达式(
的函数表达式(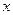 表示投入市场的第
表示投入市场的第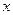 天);
天);
(Ⅱ)若销售量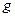 (
(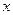 )与时间
)与时间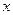 的函数关系是
的函数关系是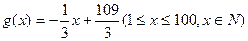 ,求日销售额的最大值,并求第几天销售额最高?
,求日销售额的最大值,并求第几天销售额最高?
推荐套卷
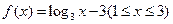 ,设
,设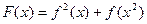

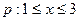 ,条件
,条件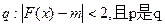 的充分条件,求实数m的取值范围.
的充分条件,求实数m的取值范围. 

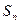 为数列
为数列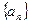 的前
的前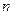 项和,
项和,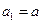 ,
,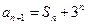 ,
,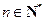 .
.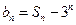 ,求数列
,求数列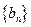 的通项公式;
的通项公式;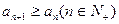 ,求
,求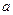 的取值范围.
的取值范围. 为数列
为数列 的前
的前 项和,已知
项和,已知
 时,
时, 是等比数列;
是等比数列; 的通项公式
的通项公式 的首项
的首项 ,
, ,
, ….证明:数列
….证明:数列 是等比数列;
是等比数列; 和
和 满足:
满足: ,
, ,
, ,其中
,其中 为实数,
为实数, .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号