已知函数
(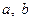 为实数,
为实数,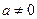 ,
,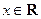 ),
),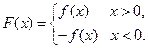
(Ⅰ)若 ,且函数
,且函数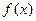 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当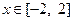 时,
时,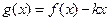 是单调函数,求实数
是单调函数,求实数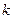
的取值范围;
(Ⅲ)设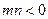 ,
,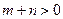 ,
,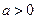 ,且函数
,且函数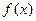 为偶函数,判断
为偶函数,判断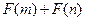 是
是
否大于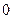 ?
?
相关知识点
推荐套卷
已知函数
(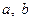 为实数,
为实数,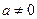 ,
,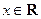 ),
),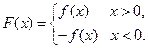
(Ⅰ)若 ,且函数
,且函数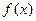 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当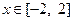 时,
时,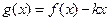 是单调函数,求实数
是单调函数,求实数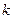
的取值范围;
(Ⅲ)设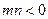 ,
,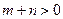 ,
,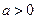 ,且函数
,且函数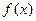 为偶函数,判断
为偶函数,判断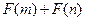 是
是
否大于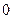 ?
?