（本小题满分16分）
设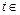
R，m，n都是不为1的正数，函数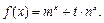
（1）若m，n满足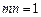
，请判断函数
是否具有奇偶性. 如果具有，求出相
应的t的值；如果不具有，请说明理由；
（2）若
，且
，请判断函数的图象是否具有对称性. 如果具
有，请求出对称轴方程或对称中心坐标；若不具有，请说明理由.
中，底面
是矩形．已知
．
平面
；
；
的大小为
，求
的值．
与定直线
，过 
点的直线
与
交于第一象限
点，与x轴正半轴交于点
，求使
面积最小的直线
的最小值及取最小值时的x、y的值.推荐套卷
（本小题满分16分）
设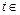R，m，n都是不为1的正数，函数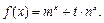
（1）若m，n满足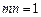，请判断函数是否具有奇偶性. 如果具有，求出相
应的t的值；如果不具有，请说明理由；
（2）若，且，请判断函数的图象是否具有对称性. 如果具
有，请求出对称轴方程或对称中心坐标；若不具有，请说明理由.
粤公网安备 44130202000953号