如图，正方形ABCD的边长是2，M是AD的中点．点E从点A出发，沿AB运动到点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．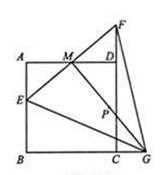
（1）设AE=x时，△EGF面积为y．求y关于x的函数关系式，并填写自变量x的取值范围；
（2）P是MG的中点，请直接写出点P运动路线的长．
相关试题
，其中
中，
， 
平分
，与
相交于点
，延长
到
，使
，
；
交
于
，且
，求证：
；
是
边的中点，连结
与
相交于点
．
，
,
之间的数量关系，并证明你的结论．
相关知识点
推荐套卷
如图，正方形ABCD的边长是2，M是AD的中点．点E从点A出发，沿AB运动到点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．
（1）设AE=x时，△EGF面积为y．求y关于x的函数关系式，并填写自变量x的取值范围；
（2）P是MG的中点，请直接写出点P运动路线的长．
粤公网安备 44130202000953号