(本小题满分14分)
已知:对于数列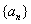 ,定义
,定义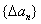 为数列
为数列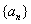 的一阶差分数列,其中
的一阶差分数列,其中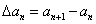 ,
,
(1)若数列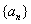 的通项公式
的通项公式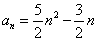 (
(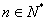 ),求:数列
),求:数列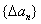 的通项公式;
的通项公式;
(2)若数列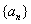 的首项是1,且满足
的首项是1,且满足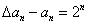 ,
,
①设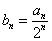 ,求证:数列
,求证:数列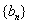 是等差数列,并求数列
是等差数列,并求数列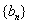 的通项公式;
的通项公式;
②求:数列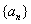 的通项公式及前
的通项公式及前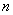 项和
项和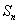
推荐套卷
(本小题满分14分)
已知:对于数列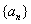 ,定义
,定义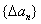 为数列
为数列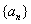 的一阶差分数列,其中
的一阶差分数列,其中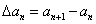 ,
,
(1)若数列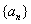 的通项公式
的通项公式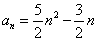 (
(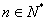 ),求:数列
),求:数列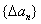 的通项公式;
的通项公式;
(2)若数列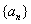 的首项是1,且满足
的首项是1,且满足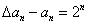 ,
,
①设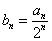 ,求证:数列
,求证:数列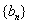 是等差数列,并求数列
是等差数列,并求数列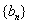 的通项公式;
的通项公式;
②求:数列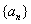 的通项公式及前
的通项公式及前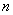 项和
项和