已知椭圆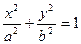
(a>b>0)
（1）当椭圆的离心率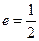
，一条准线方程为x＝4 时，求椭圆方程；
（2）设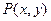
是椭圆上一点，在（1）的条件下，求
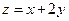的最大值及相应的P点坐标。
（3）过B(0,－b)作椭圆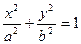(a>b>0)的弦，若弦长的最大值不是2b，求椭圆离心率的取值范围。
相关试题
是定义在
上的函数，
，且
，总有
恒成立．
是奇函数；
，有
，
，求：
及
；
的最小值．
的最大值，及当取最大值时x的取值集合。
的最大值.
的前 
项 和为 
已知 
，证明 数 列 
是等比数列
（其中
为常量，且
）的图象经过点A（1，6）、B（3，24）。
的解析式；
时恒成立，求实数
的取值范围。
的图象关于原点成中心对称, 试判断
在区间
上的单调性,并证明你的结论.推荐套卷
已知椭圆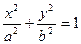(a>b>0)
（1）当椭圆的离心率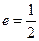，一条准线方程为x＝4 时，求椭圆方程；
（2）设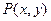是椭圆上一点，在（1）的条件下，求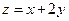的最大值及相应的P点坐标。
（3）过B(0,－b)作椭圆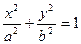(a>b>0)的弦，若弦长的最大值不是2b，求椭圆离心率的取值范围。
粤公网安备 44130202000953号