(本小题满分12分)
如图,正方形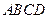 所在平面与圆
所在平面与圆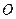 所在平面相交于
所在平面相交于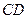 ,线段
,线段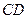 为圆
为圆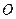 的弦,
的弦,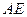 垂直于圆
垂直于圆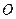 所在平面,垂足
所在平面,垂足 是圆
是圆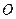 上异于
上异于 .
.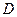 的点,
的点, ,圆
,圆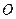 的直径为9.
的直径为9.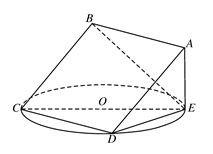
(I)求证:平面 平面
平面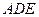 ;
;
(II)求二面角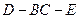 的平面角的正切值.
的平面角的正切值.
推荐套卷
(本小题满分12分)
如图,正方形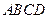 所在平面与圆
所在平面与圆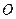 所在平面相交于
所在平面相交于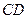 ,线段
,线段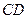 为圆
为圆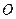 的弦,
的弦,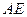 垂直于圆
垂直于圆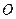 所在平面,垂足
所在平面,垂足 是圆
是圆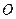 上异于
上异于 .
.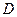 的点,
的点, ,圆
,圆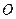 的直径为9.
的直径为9.
(I)求证:平面 平面
平面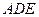 ;
;
(II)求二面角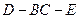 的平面角的正切值.
的平面角的正切值.