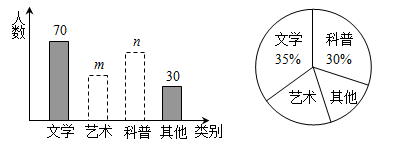
为了丰富校园文化生活，某校计划在午间校园广播台播放“百家讲坛”的部分内容．为了了解学生的喜好，抽取若干名学生进行问卷调查（每人只选一项内容），整理调查结果，绘制统计图如下： 
请根据统计图提供的信息回答以下问题：
（1）抽取的学生数为_______名；
（2）该校有3000名学生，估计喜欢收听易中天《品三国》的学生有_______名；
（3）估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的_ ___%；
（4）你认为上述估计合理吗？理由是什么？
相关试题
（本小题满分6分）
（1）画图，已知线段a和锐角
，求作Rt△ABC，使它的一边为a，一锐角为（不写作法，要保留作图痕迹，作出其中一个满足条件的直角三角形即可）。
（2）回答问题：
1满足上述条件的大小不同的共有种。
|
2若＝
，求最大的Rt△ABC的面积。
（本小题满分6分）
能否在图中的四个圆圈内填入4个互不相同的数，使得任意两个圆圈中所填的数的平方和等于另外两个圆圈中所填数的平方和？如果能填，请填出一个例；如果不能填，请说明理由。
|
有解，求k的取值范围。
，
，
，……
，试求
的值。相关知识点
推荐套卷
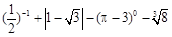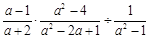粤公网安备 44130202000953号