(本小题满分12分)
如图, 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆 上,且
上,且 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, 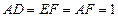 .
.
(Ⅰ)求四棱锥 的体积
的体积 ;(Ⅱ)求证:平面
;(Ⅱ)求证:平面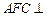 平面
平面 ;
;
(Ⅲ)在线段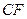 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,并说明理由.
,并说明理由.
推荐套卷
(本小题满分12分)
如图, 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆 上,且
上,且 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, 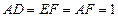 .
.
(Ⅰ)求四棱锥 的体积
的体积 ;(Ⅱ)求证:平面
;(Ⅱ)求证:平面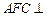 平面
平面 ;
;
(Ⅲ)在线段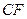 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,并说明理由.
,并说明理由.