（本小题满分12分）已知函数
，
.
（1）若函数
是单调递增函数，求实数
的取值范围；
（2）当
时，两曲线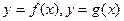
有公共点P，设曲线
在P处的切线分别为
，若切线与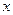
轴围成一个等腰三角形，求P点坐标和
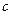的值；
（3）当
时，讨论关于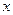的方程
的根的个数。
相关试题
中，
，斜边
．
可以通过
为轴旋转得到，且二面角
是直二面角．动点
在斜边
上．
平面
；
与平面
中，底面
是正方形，侧棱
⊥底面
，
是
的中点，作
交
于点
．
平面
；
平面
．
与
都是边长为
的正方形，点
是
的中点，
平面
平面
;
的体积.
中,
,
，求：
与
所成角的余弦值； 
的距离．
，函数
是区间
上的减函数.
的最大值；
恒成立，求
的取值范围；
的方程
的根的个数．推荐套卷
（本小题满分12分）已知函数，.
（1）若函数是单调递增函数，求实数的取值范围；
（2）当时，两曲线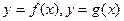有公共点P，设曲线在P处的切线分别为，若切线与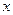轴围成一个等腰三角形，求P点坐标和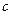的值；
（3）当时，讨论关于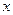的方程的根的个数。
粤公网安备 44130202000953号