已知数列 的前
的前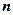 项和为
项和为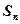 ,则关于
,则关于 的命题(其中
的命题(其中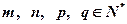 )。
)。
①若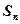 是关于
是关于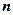 的二次函数,则
的二次函数,则 是等差数列;
是等差数列;
② ;
;
③若 是等比数列,且
是等比数列,且 ,则
,则 ;
;
④若 是等差数列,且
是等差数列,且 ,则
,则 ;
;
⑤若 是等差数列,则
是等差数列,则 。其中正确的有( )个。
。其中正确的有( )个。
| A.2 | B.3 | C.4 | D.5 |
相关知识点
推荐套卷
已知数列 的前
的前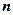 项和为
项和为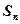 ,则关于
,则关于 的命题(其中
的命题(其中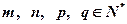 )。
)。
①若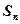 是关于
是关于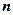 的二次函数,则
的二次函数,则 是等差数列;
是等差数列;
② ;
;
③若 是等比数列,且
是等比数列,且 ,则
,则 ;
;
④若 是等差数列,且
是等差数列,且 ,则
,则 ;
;
⑤若 是等差数列,则
是等差数列,则 。其中正确的有( )个。
。其中正确的有( )个。
| A.2 | B.3 | C.4 | D.5 |