已知数列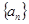
满足
，给出下列命题：
①当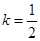
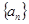时，数列为递减数列
②当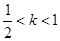
时，数列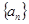不一定有最大项
③当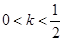
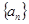时，数列为递减数列
④当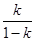
为正整数时，数列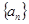必有两项相等的最大项
其中真命题的个数为（ ）
| A．0 | B．1 | C．2 | D．3 |
相关试题
是
上的增函数，
，则（）
，
是两个集合，则“
”是“
”的（）
，
，则
（ ）
推荐套卷
已知数列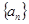满足，给出下列命题：
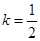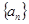①当时，数列为递减数列
②当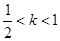时，数列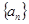不一定有最大项
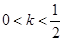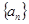③当时，数列为递减数列
④当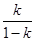为正整数时，数列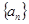必有两项相等的最大项
其中真命题的个数为（ ）
| A．0 | B．1 | C．2 | D．3 |
粤公网安备 44130202000953号