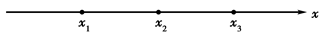本题满分12分）
在一条笔直的工艺流水线上有三个工作台，将工艺流水线用如图所示的数轴表示，各工作台的坐标分别为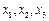
，每个工作台上有若干名工人.现要在
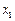与
之间修建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短.
（1）若每个工作台上只有一名工人，试确定供应站的位置；
（2）设三个工作台从左到右的人数依次为2，1，3，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值.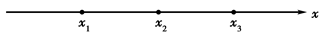
相关试题
若对任意x1∈[0,1]，存在x2∈[1,2]，使
，求实数a的取值范围？
在区间
上单调递减，求
的取值范围；
时，
恒成立，求
的最大值及此时
,过点Ｐ
的直线
与曲线
相切，求
，当
时，
在１,４上的最小值为
，求
其中
在
中，
分别是角的对边，且
．
，
，求
推荐套卷
本题满分12分）
在一条笔直的工艺流水线上有三个工作台，将工艺流水线用如图所示的数轴表示，各工作台的坐标分别为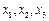，每个工作台上有若干名工人.现要在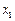与之间修建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短.
（1）若每个工作台上只有一名工人，试确定供应站的位置；
（2）设三个工作台从左到右的人数依次为2，1，3，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值.
粤公网安备 44130202000953号