(本小题15分)
已知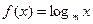
（m为常数，m>0且
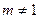）,设
是首项为4，公差为2的等差数列.
（1）求证：数列{an}是等比数列；
（2）若bn=an·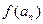
，且数列{bn}的前n项和Sn，当
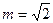时，求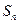
；
（3）若cn=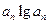
，问是否存在m，使得{cn}中每一项恒小于它后面的项？若存在，
求出m的范围；若不存在，说明理由.
相关试题
，函数
的两个零点为m，n（m＜n）．
，比较f（x）与m的大小．
上一点Q（4，m）到焦点F的距离为5．
，求直线L的方程．
，
．
中，
，
，
，
＝
，求：
的值；
的大小．
为奇函数，
的值；
的解集．推荐套卷
(本小题15分)
已知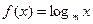（m为常数，m>0且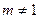）,设是首项为4，公差为2的等差数列.
（1）求证：数列{an}是等比数列；
（2）若bn=an·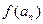，且数列{bn}的前n项和Sn，当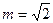时，求；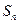
（3）若cn=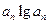，问是否存在m，使得{cn}中每一项恒小于它后面的项？若存在，
求出m的范围；若不存在，说明理由.
粤公网安备 44130202000953号