在平面直角坐标系xOy中,已知对于任意实数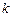 ,直线
,直线 恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为
恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为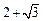 .
.
(1)求椭圆C的方程;
(2)设(m,n)是椭圆C上的任意一点,圆O: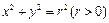 与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
推荐套卷
在平面直角坐标系xOy中,已知对于任意实数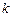 ,直线
,直线 恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为
恒过定点F. 设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为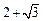 .
.
(1)求椭圆C的方程;
(2)设(m,n)是椭圆C上的任意一点,圆O: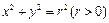 与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.