(本小题满分12分)
小明参加一次比赛,比赛共设三关。第一、二关各有两个问题,两个问题全答对,可进入下一关。第三关有三个问题,只要答对其中两个问题,则闯关成功。每过一关可一次性获得价值分别为100、300、500元的奖励。小明对三关中每个问题回答正确的概率依次为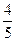 、
、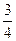 、
、 ,且每个问题回答正确
,且每个问题回答正确 与否相互独立。
与否相互独立。
(1)求小明过第一关但未过第二关的概率;
(2)用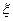 表示小明所获得奖品的价值,求
表示小明所获得奖品的价值,求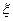 的分布列和期望。
的分布列和期望。
推荐套卷
(本小题满分12分)
小明参加一次比赛,比赛共设三关。第一、二关各有两个问题,两个问题全答对,可进入下一关。第三关有三个问题,只要答对其中两个问题,则闯关成功。每过一关可一次性获得价值分别为100、300、500元的奖励。小明对三关中每个问题回答正确的概率依次为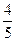 、
、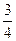 、
、 ,且每个问题回答正确
,且每个问题回答正确 与否相互独立。
与否相互独立。
(1)求小明过第一关但未过第二关的概率;
(2)用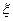 表示小明所获得奖品的价值,求
表示小明所获得奖品的价值,求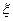 的分布列和期望。
的分布列和期望。