如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
相关知识点
推荐套卷
 , 6 ,
, 6 , ,0,
,0,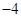 ,写出整数的和与分数的积的差
,写出整数的和与分数的积的差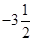 ,
,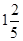 ,
,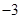 ,
, 这六个数中,负数有m个,整数有n个,非负数有k个,求
这六个数中,负数有m个,整数有n个,非负数有k个,求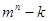 的值。
的值。 ,
,
 , 0, -|-2︳, 2.5 |-3︳
, 0, -|-2︳, 2.5 |-3︳ 中,直线AB交
中,直线AB交 轴于A(2,0),交
轴于A(2,0),交 轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA. 的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
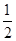 AB.
AB.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号