(本题12分)某汽车厂有一条价值为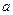 万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值
万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值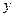 万元与技术改造投入
万元与技术改造投入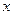 万元之间满足:①
万元之间满足:①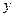 与
与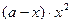 成正比;②当
成正比;②当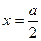 时,
时,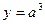 ,并且技术改造投入满足
,并且技术改造投入满足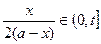 ,其中
,其中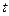 为常数且
为常数且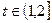 。
。
(1)求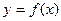 表达式及定义域;
表达式及定义域;
(2)求出产品增加值的最大值及相应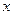 的值。
的值。
推荐套卷
(本题12分)某汽车厂有一条价值为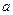 万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值
万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值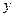 万元与技术改造投入
万元与技术改造投入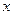 万元之间满足:①
万元之间满足:①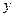 与
与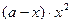 成正比;②当
成正比;②当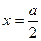 时,
时,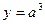 ,并且技术改造投入满足
,并且技术改造投入满足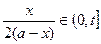 ,其中
,其中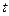 为常数且
为常数且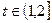 。
。
(1)求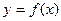 表达式及定义域;
表达式及定义域;
(2)求出产品增加值的最大值及相应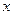 的值。
的值。